Vavr User Guide

1. Introduction

Vavr (formerly called Javaslang) is a functional library for Java 8+ that provides persistent data types and functional control structures.

1.1. Functional Data Structures in Java 8 with Vavr

Java 8’s lambdas (λ) empower us to create wonderful API’s. They incredibly increase the expressiveness of the language.

Vavr leveraged lambdas to create various new features based on functional patterns. One of them is a functional collection library that is intended to be a replacement for Java’s standard collections.

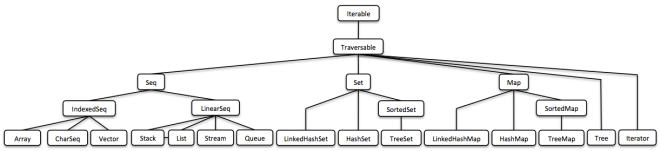
(This is just a bird’s view, you will find a human-readable version below.)

1.2. Functional Programming

Before we deep-dive into the details about the data structures I want to talk about some basics. This will make it clear why I created Vavr and specifically new Java collections.

1.2.1. Side-Effects

Java applications are typically plentiful of side-effects. They mutate some sort of state, maybe the outer world. Common side effects are changing objects or variables in place, printing to the console, writing to a log file or to a database. Side-effects are considered harmful if they affect the semantics of our program in an undesirable way.

For example, if a function throws an exception and this exception is interpreted, it is considered as side-effect that affects our program. Furthermore exceptions are like non-local goto-statements. They break the normal control-flow. However, real-world applications do perform side-effects.

int divide(int dividend, int divisor) {
    // throws if divisor is zero
    return dividend / divisor;
}

In a functional setting we are in the favorable situation to encapsulate the side-effect in a Try:

// = Success(result) or Failure(exception)
Try<Integer> divide(Integer dividend, Integer divisor) {
    return Try.of(() -> dividend / divisor);
}

This version of divide does not throw any exception anymore. We made the possible failure explicit by using the type Try.

1.2.2. Referential Transparency

A function, or more generally an expression, is called referentially transparent if a call can be replaced by its value without affecting the behavior of the program. Simply spoken, given the same input the output is always the same.

// not referentially transparent
Math.random();

// referentially transparent
Math.max(1, 2);

A function is called pure if all expressions involved are referentially transparent. An application composed of pure functions will most probably just work if it compiles. We are able to reason about it. Unit tests are easy to write and debugging becomes a relict of the past.

1.2.3. Thinking in Values

Rich Hickey, the creator of Clojure, gave a great talk about The Value of Values. The most interesting values are immutable values. The main reason is that immutable values

are inherently thread-safe and hence do not need to be synchronized
are stable regarding equals and hashCode and thus are reliable hash keys
do not need to be cloned
behave type-safe when used in unchecked covariant casts (Java-specific)
The key to a better Java is to use immutable values paired with referentially transparent functions.

Vavr provides the necessary controls and collections to accomplish this goal in every-day Java programming.

1.3. Data Structures in a Nutshell

Vavr’s collection library comprises of a rich set of functional data structures built on top of lambdas. The only interface they share with Java’s original collections is Iterable. The main reason is that the mutator methods of Java’s collection interfaces do not return an object of the underlying collection type.

We will see why this is so essential by taking a look at the different types of data structures.

1.3.1. Mutable Data Structures

Java is an object-oriented programming language. We encapsulate state in objects to achieve data hiding and provide mutator methods to control the state. The Java collections framework (JCF) is built upon this idea.

interface Collection<E> {
    // removes all elements from this collection
    void clear();
}

Today I comprehend a void return type as a smell. It is evidence that side-effects take place, state is mutated. Shared mutable state is an important source of failure, not only in a concurrent setting.

1.3.2. Immutable Data Structures

Immutable data structures cannot be modified after their creation. In the context of Java they are widely used in the form of collection wrappers.

List<String> list = Collections.unmodifiableList(otherList);

// Boom!
list.add("why not?");

There are various libraries that provide us with similar utility methods. The result is always an unmodifiable view of the specific collection. Typically it will throw at runtime when we call a mutator method.

1.3.3. Persistent Data Structures

A persistent data structure does preserve the previous version of itself when being modified and is therefore effectively immutable. Fully persistent data structures allow both updates and queries on any version.

Many operations perform only small changes. Just copying the previous version wouldn’t be efficient. To save time and memory, it is crucial to identify similarities between two versions and share as much data as possible.

This model does not impose any implementation details. Here come functional data structures into play.

1.4. Functional Data Structures

Also known as purely functional data structures, these are immutable and persistent. The methods of functional data structures are referentially transparent.

Vavr features a wide range of the most-commonly used functional data structures. The following examples are explained in-depth.

1.4.1. Linked List

One of the most popular and also simplest functional data structures is the (singly) linked List. It has a head element and a tail List. A linked List behaves like a Stack which follows the last in, first out (LIFO) method.

In Vavr we instantiate a List like this:

// = List(1, 2, 3)
List<Integer> list1 = List.of(1, 2, 3);

Each of the List elements forms a separate List node. The tail of the last element is Nil, the empty List.

This enables us to share elements across different versions of the List.

// = List(0, 2, 3)
List<Integer> list2 = list1.tail().prepend(0);

The new head element 0 is linked to the tail of the original List. The original List remains unmodified.

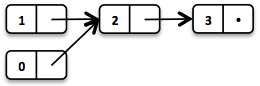
These operations take place in constant time, in other words they are independent of the List size. Most of the other operations take linear time. In Vavr this is expressed by the interface LinearSeq, which we may already know from Scala.

If we need data structures that are queryable in constant time, Vavr offers Array and Vector. Both have random access capabilities.

The Array type is backed by a Java array of objects. Insert and remove operations take linear time. Vector is in-between Array and List. It performs well in both areas, random access and modification.

In fact the linked List can also be used to implement a Queue data structure.

1.4.2. Queue

A very efficient functional Queue can be implemented based on two linked Lists. The front List holds the elements that are dequeued, the rear List holds the elements that are enqueued. Both operations enqueue and dequeue perform in O(1).

Queue<Integer> queue = Queue.of(1, 2, 3)
                            .enqueue(4)
                            .enqueue(5);

The initial Queue is created of three elements. Two elements are enqueued on the rear List.

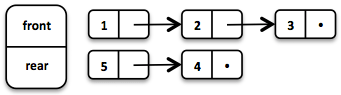
If the front List runs out of elements when dequeueing, the rear List is reversed and becomes the new front List.

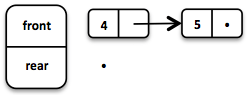
When dequeueing an element we get a pair of the first element and the remaining Queue. It is necessary to return the new version of the Queue because functional data structures are immutable and persistent. The original Queue is not affected.

Queue<Integer> queue = Queue.of(1, 2, 3);

// = (1, Queue(2, 3))
Tuple2<Integer, Queue<Integer>> dequeued =
        queue.dequeue();

What happens when the Queue is empty? Then dequeue() will throw a NoSuchElementException. To do it the functional way we would rather expect an optional result.

// = Some((1, Queue()))
Queue.of(1).dequeueOption();

// = None
Queue.empty().dequeueOption();

An optional result may be further processed, regardless if it is empty or not.

// = Queue(1)
Queue<Integer> queue = Queue.of(1);

// = Some((1, Queue()))
Option<Tuple2<Integer, Queue<Integer>>> dequeued =
        queue.dequeueOption();

// = Some(1)
Option<Integer> element = dequeued.map(Tuple2::_1);

// = Some(Queue())
Option<Queue<Integer>> remaining =
        dequeued.map(Tuple2::_2);

1.4.3. Sorted Set

Sorted Sets are data structures that are more frequently used than Queues. We use binary search trees to model them in a functional way. These trees consist of nodes with up to two children and values at each node.

We build binary search trees in the presence of an ordering, represented by an element Comparator. All values of the left subtree of any given node are strictly less than the value of the given node. All values of the right subtree are strictly greater.

// = TreeSet(1, 2, 3, 4, 6, 7, 8)
SortedSet<Integer> xs = TreeSet.of(6, 1, 3, 2, 4, 7, 8);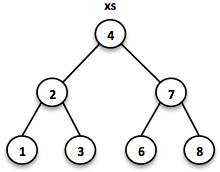

Searches on such trees run in O(log n) time. We start the search at the root and decide if we found the element. Because of the total ordering of the values we know where to search next, in the left or in the right branch of the current tree.

// = TreeSet(1, 2, 3);
SortedSet<Integer> set = TreeSet.of(2, 3, 1, 2);

// = TreeSet(3, 2, 1);
Comparator<Integer> c = (a, b) -> b - a;
SortedSet<Integer> reversed = TreeSet.of(c, 2, 3, 1, 2);

Most tree operations are inherently recursive. The insert function behaves similarly to the search function. When the end of a search path is reached, a new node is created and the whole path is reconstructed up to the root. Existing child nodes are referenced whenever possible. Hence the insert operation takes O(log n) time and space.

// = TreeSet(1, 2, 3, 4, 5, 6, 7, 8)
SortedSet<Integer> ys = xs.add(5);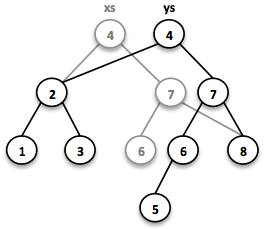

In order to maintain the performance characteristics of a binary search tree it needs to be kept balanced. All paths from the root to a leaf need to have roughly the same length.

In Vavr we implemented a binary search tree based on a Red/Black Tree. It uses a specific coloring strategy to keep the tree balanced on inserts and deletes. To read more about this topic please refer to the book Purely Functional Data Structures by Chris Okasaki.

1.5. State of the Collections

Generally we are observing a convergence of programming languages. Good features make it, other disappear. But Java is different, it is bound forever to be backward compatible. That is a strength but also slows down evolution.

Lambda brought Java and Scala closer together, yet they are still so different. Martin Odersky, the creator of Scala, recently mentioned in his BDSBTB 2015 keynote the state of the Java 8 collections.

He described Java’s Stream as a fancy form of an Iterator. The Java 8 Stream API is an example of a lifted collection. What it does is to define a computation and link it to a specific collection in another explicit step.

// i + 1
i.prepareForAddition()
 .add(1)
 .mapBackToInteger(Mappers.toInteger())

This is how the new Java 8 Stream API works. It is a computational layer above the well known Java collections.

// = ["1", "2", "3"] in Java 8
Arrays.asList(1, 2, 3)
      .stream()
      .map(Object::toString)
      .collect(Collectors.toList())

Vavr is greatly inspired by Scala. This is how the above example should have been in Java 8.

// = Stream("1", "2", "3") in Vavr
Stream.of(1, 2, 3).map(Object::toString)

Within the last year we put much effort into implementing the Vavr collection library. It comprises the most widely used collection types.

1.5.1. Seq

We started our journey by implementing sequential types. We already described the linked List above. Stream, a lazy linked List, followed. It allows us to process possibly infinite long sequences of elements.

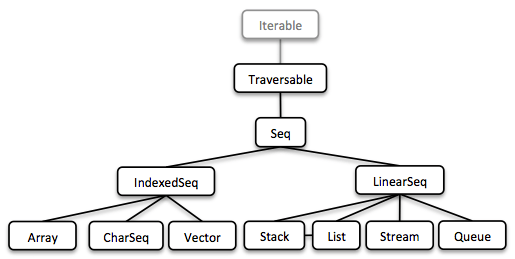
All collections are Iterable and hence could be used in enhanced for-statements.

for (String s : List.of("Java", "Advent")) {
    // side effects and mutation
}

We could accomplish the same by internalizing the loop and injecting the behavior using a lambda.

List.of("Java", "Advent").forEach(s -> {
    // side effects and mutation
});

Anyway, as we previously saw we prefer expressions that return a value over statements that return nothing. By looking at a simple example, soon we will recognize that statements add noise and divide what belongs together.

String join(String... words) {
    StringBuilder builder = new StringBuilder();
    for(String s : words) {
        if (builder.length() > 0) {
            builder.append(", ");
        }
        builder.append(s);
    }
    return builder.toString();
}

The Vavr collections provide us with many functions to operate on the underlying elements. This allows us to express things in a very concise way.

String join(String... words) {
    return List.of(words)
               .intersperse(", ")
               .foldLeft(new StringBuilder(), StringBuilder::append)
               .toString();
}

Most goals can be accomplished in various ways using Vavr. Here we reduced the whole method body to fluent function calls on a List instance. We could even remove the whole method and directly use our List to obtain the computation result.

List.of(words).mkString(", ");

In a real world application we are now able to drastically reduce the number of lines of code and hence lower the risk of bugs.

1.5.2. Set and Map

Sequences are great. But to be complete, a collection library also needs different types of Sets and Maps.

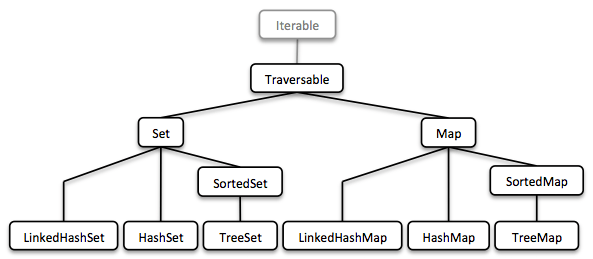
We described how to model sorted Sets with binary tree structures. A sorted Map is nothing else than a sorted Set containing key-value pairs and having an ordering for the keys.

The HashMap implementation is backed by a Hash Array Mapped Trie (HAMT). Accordingly the HashSet is backed by a HAMT containing key-key pairs.

Our Map does not have a special Entry type to represent key-value pairs. Instead we use Tuple2 which is already part of Vavr. The fields of a Tuple are enumerated.

// = (1, "A")
Tuple2<Integer, String> entry = Tuple.of(1, "A");

Integer key = entry._1;
String value = entry._2;

Maps and Tuples are used throughout Vavr. Tuples are inevitable to handle multi-valued return types in a general way.

// = HashMap((0, List(2, 4)), (1, List(1, 3)))
List.of(1, 2, 3, 4).groupBy(i -> i % 2);

// = List((a, 0), (b, 1), (c, 2))
List.of('a', 'b', 'c').zipWithIndex();

At Vavr, we explore and test our library by implementing the 99 Euler Problems. It is a great proof of concept. Please don’t hesitate to send pull requests.

2. Getting started

Projects that include Vavr need to target Java 1.8 at minimum.

The .jar is available at Maven Central.

2.1. Gradle

dependencies {
    compile "io.vavr:vavr:0.10.5"
}

Gradle 7+

dependencies {
    implementation "io.vavr:vavr:0.10.5"
}

2.2. Maven

<dependencies>
    <dependency>
        <groupId>io.vavr</groupId>
        <artifactId>vavr</artifactId>
        <version>0.10.5</version>
    </dependency>
</dependencies>

2.3. Standalone

Because Vavr does not depend on any libraries (other than the JVM) you can easily add it as standalone .jar to your classpath.

2.4. Snapshots

Developer versions can be found here.

2.4.1. Gradle

Add the additional snapshot repository to your build.gradle:

repositories {
    (...)
    maven { url "https://oss.sonatype.org/content/repositories/snapshots" }
}

2.4.2. Maven

Ensure that your ~/.m2/settings.xml contains the following:

<profiles>
    <profile>
        <id>allow-snapshots</id>
        <activation>
            <activeByDefault>true</activeByDefault>
        </activation>
        <repositories>
            <repository>
                <id>snapshots-repo</id>
                <url>https://oss.sonatype.org/content/repositories/snapshots</url>
                <releases>
                    <enabled>false</enabled>
                </releases>
                <snapshots>
                    <enabled>true</enabled>
                </snapshots>
            </repository>
        </repositories>
    </profile>
</profiles>

3. Usage Guide

Vavr comes along with well-designed representations of some of the most basic types which apparently are missing or rudimentary in Java: Tuple, Value and λ.
In Vavr, everything is built upon these three basic building blocks:

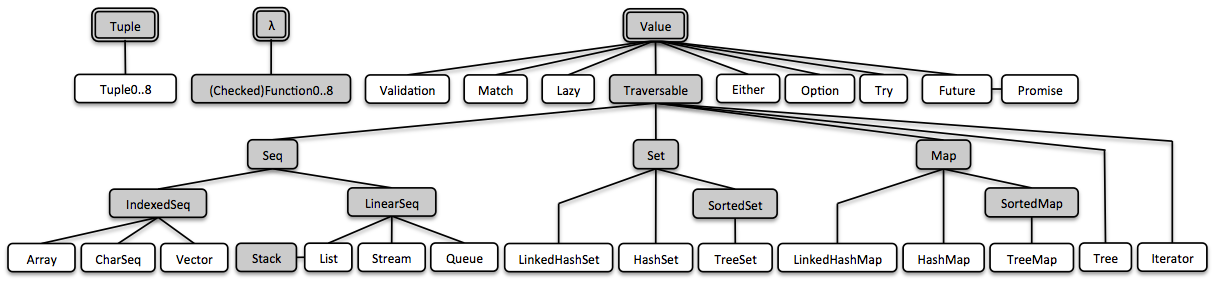
3.1. Tuples

Java is missing a general notion of tuples. A Tuple combines a fixed number of elements together so that they can be passed around as a whole. Unlike an array or list, a tuple can hold objects with different types, but they are also immutable.
Tuples are of type Tuple1, Tuple2, Tuple3 and so on. There currently is an upper limit of 8 elements. To access elements of a tuple t, you can use method t._1 to access the first element, t._2 to access the second, and so on.

3.1.1. Create a tuple

Here is an example of how to create a tuple holding a String and an Integer:

// (Java, 8)
Tuple2<String, Integer> java8 = Tuple.of("Java", 8); (1)

// "Java"
String s = java8._1; (2)

// 8
Integer i = java8._2; (3)

1	A tuple is created via the static factory method `Tuple.of()`
2	Get the 1st element of this tuple.
3	Get the 2nd element of this tuple.

3.1.2. Map a tuple component-wise

The component-wise map evaluates a function per element in the tuple, returning another tuple.

// (vavr, 1)
Tuple2<String, Integer> that = java8.map(
        s -> s.substring(2) + "vr",
        i -> i / 8
);

3.1.3. Map a tuple using one mapper

It is also possible to map a tuple using one mapping function.

// (vavr, 1)
Tuple2<String, Integer> that = java8.map(
        (s, i) -> Tuple.of(s.substring(2) + "vr", i / 8)
);

3.1.4. Transform a tuple

Transform creates a new type based on the tuple’s contents.

// "vavr 1"
String that = java8.apply(
        (s, i) -> s.substring(2) + "vr " + i / 8
);

3.2. Functions

Functional programming is all about values and transformation of values using functions. Java 8 just provides a Function which accepts one parameter and a BiFunction which accepts two parameters. Vavr provides functions up to a limit of 8 parameters. The functional interfaces are of called Function0, Function1, Function2, Function3 and so on. If you need a function which throws a checked exception you can use CheckedFunction1, CheckedFunction2 and so on.
The following lambda expression creates a function to sum two integers:

// sum.apply(1, 2) = 3
Function2<Integer, Integer, Integer> sum = (a, b) -> a + b;

This is a shorthand for the following anonymous class definition:

Function2<Integer, Integer, Integer> sum = new Function2<Integer, Integer, Integer>() {
    @Override
    public Integer apply(Integer a, Integer b) {
        return a + b;
    }
};

You can also use the static factory method Function3.of(…) to a create a function from any method reference.

Function3<String, String, String, String> function3 =
        Function3.of(this::methodWhichAccepts3Parameters);

In fact Vavr functional interfaces are Java 8 functional interfaces on steroids. They also provide features like:

Composition
Lifting
Currying
Memoization

3.2.1. Composition

You can compose functions. In mathematics, function composition is the application of one function to the result of another to produce a third function. For instance, the functions f : X → Y and g : Y → Z can be composed to yield a function h: g(f(x)) which maps X → Z.
You can use either andThen:

Function1<Integer, Integer> plusOne = a -> a + 1;
Function1<Integer, Integer> multiplyByTwo = a -> a * 2;

Function1<Integer, Integer> add1AndMultiplyBy2 = plusOne.andThen(multiplyByTwo);

then(add1AndMultiplyBy2.apply(2)).isEqualTo(6);

or compose:

Function1<Integer, Integer> add1AndMultiplyBy2 = multiplyByTwo.compose(plusOne);

then(add1AndMultiplyBy2.apply(2)).isEqualTo(6);

3.2.2. Lifting

You can lift a partial function into a total function that returns an Option result. The term partial function comes from mathematics. A partial function from X to Y is a function f: X′ → Y, for some subset X′ of X. It generalizes the concept of a function f: X → Y by not forcing f to map every element of X to an element of Y. That means a partial function works properly only for some input values. If the function is called with a disallowed input value, it will typically throw an exception.

The following method divide is a partial function that only accepts non-zero divisors.

Function2<Integer, Integer, Integer> divide = (a, b) -> a / b;

We use lift to turn divide into a total function that is defined for all inputs.

Function2<Integer, Integer, Option<Integer>> safeDivide = Function2.lift(divide);

// = None
Option<Integer> i1 = safeDivide.apply(1, 0); (1)

// = Some(2)
Option<Integer> i2 = safeDivide.apply(4, 2); (2)

1	A lifted function returns `None` instead of throwing an exception, if the function is invoked with disallowed input values.
2	A lifted function returns `Some`, if the function is invoked with allowed input values.

The following method sum is a partial function that only accepts positive input values.

int sum(int first, int second) {
    if (first < 0 || second < 0) {
        throw new IllegalArgumentException("Only positive integers are allowed"); (1)
    }
    return first + second;
}

1	The function `sum` throws an `IllegalArgumentException` for negative input values.

We may lift the sum method by providing the methods reference.

Function2<Integer, Integer, Option<Integer>> sum = Function2.lift(this::sum);

// = None
Option<Integer> optionalResult = sum.apply(-1, 2); (1)

1	The lifted function catches the `IllegalArgumentException` and maps it to `None`.

3.2.3. Partial application

Partial application allows you to derive a new function from an existing one by fixing some values. You can fix one or more parameters, and the number of fixed parameters defines the arity of the new function such that new arity = (original arity - fixed parameters). The parameters are bound from left to right.

Function2<Integer, Integer, Integer> sum = (a, b) -> a + b;
Function1<Integer, Integer> add2 = sum.apply(2); (1)

then(add2.apply(4)).isEqualTo(6);

1	The first parameter `a` is fixed to the value 2.

This can be demonstrated by fixing the first three parameters of a Function5, resulting in a Function2.

Function5<Integer, Integer, Integer, Integer, Integer, Integer> sum = (a, b, c, d, e) -> a + b + c + d + e;
Function2<Integer, Integer, Integer> add6 = sum.apply(2, 3, 1); (1)

then(add6.apply(4, 3)).isEqualTo(13);

1	The `a`, `b` and `c` parameters are fixed to the values 2, 3 and 1 respectively.

Partial application differs from Currying, as will be explored in the relevant section.

3.2.4. Currying

Currying is a technique to partially apply a function by fixing a value for one of the parameters, resulting in a Function1 function that returns a Function1.

When a Function2 is curried, the result is indistinguishable from the partial application of a Function2 because both result in a 1-arity function.

Function2<Integer, Integer, Integer> sum = (a, b) -> a + b;
Function1<Integer, Integer> add2 = sum.curried().apply(2); (1)

then(add2.apply(4)).isEqualTo(6);

1	The first parameter `a` is fixed to the value 2.

You might notice that, apart from the use of .curried(), this code is identical to the 2-arity given example in Partial application. With higher-arity functions, the difference becomes clear.

Function3<Integer, Integer, Integer, Integer> sum = (a, b, c) -> a + b + c;
final Function1<Integer, Function1<Integer, Integer>> add2 = sum.curried().apply(2);(1)

then(add2.apply(4).apply(3)).isEqualTo(9);(2)

1	Note the presence of additional functions in the parameters.
2	Further calls to `apply` returns another `Function1`, apart from the final call.

3.2.5. Memoization

Memoization is a form of caching. A memoized function executes only once and then returns the result from a cache.
The following example calculates a random number on the first invocation and returns the cached number on the second invocation.

Function0<Double> hashCache =
        Function0.of(Math::random).memoized();

double randomValue1 = hashCache.apply();
double randomValue2 = hashCache.apply();

then(randomValue1).isEqualTo(randomValue2);

3.3. Values

In a functional setting we see a value as a kind of normal form, an expression which cannot be further evaluated. In Java we express this by making the state of an object final and call it immutable.
Vavr’s functional Value abstracts over immutable objects. Efficient write operations are added by sharing immutable memory between instances. What we get is thread-safety for free!

3.3.1. Option

Option is a monadic container type which represents an optional value. Instances of Option are either an instance of Some or the None.

// optional *value*, no more nulls
Option<T> option = Option.of(...);

If you’re coming to Vavr after using Java’s Optional class, there is a crucial difference. In Optional, a call to .map that results in a null will result in an empty Optional. In Vavr, it would result in a Some(null) that can then lead to a NullPointerException.

Using Optional, this scenario is valid.

Optional<String> maybeFoo = Optional.of("foo"); (1)
then(maybeFoo.get()).isEqualTo("foo");
Optional<String> maybeFooBar = maybeFoo.map(s -> (String)null)  (2)
                                       .map(s -> s.toUpperCase() + "bar");
then(maybeFooBar.isPresent()).isFalse();

1	The option is `Some("foo")`
2	The resulting option becomes empty here

Using Vavr’s Option, the same scenario will result in a NullPointerException.

Option<String> maybeFoo = Option.of("foo"); (1)
then(maybeFoo.get()).isEqualTo("foo");
try {
    maybeFoo.map(s -> (String)null) (2)
            .map(s -> s.toUpperCase() + "bar"); (3)
    Assert.fail();
} catch (NullPointerException e) {
    // this is clearly not the correct approach
}

1	The option is `Some("foo")`
2	The resulting option is `Some(null)`
3	The call to `s.toUpperCase()` is invoked on a `null`

This seems like Vavr’s implementation is broken, but in fact it’s not - rather, it adheres to the requirement of a monad to maintain computational context when calling .map. In terms of an Option, this means that calling .map on a Some will result in a Some, and calling .map on a None will result in a None. In the Java Optional example above, that context changed from a Some to a None.

This may seem to make Option useless, but it actually forces you to pay attention to possible occurrences of null and deal with them accordingly instead of unknowingly accepting them. The correct way to deal with occurrences of null is to use flatMap.

Option<String> maybeFoo = Option.of("foo"); (1)
then(maybeFoo.get()).isEqualTo("foo");
Option<String> maybeFooBar = maybeFoo.map(s -> (String)null) (2)
                                     .flatMap(s -> Option.of(s) (3)
                                                         .map(t -> t.toUpperCase() + "bar"));
then(maybeFooBar.isEmpty()).isTrue();

1	The option is `Some("foo")`
2	The resulting option is `Some(null)`
3	`s`, which is `null`, becomes `None`

Alternatively, move the .flatMap to be co-located with the the possibly null value.

Option<String> maybeFoo = Option.of("foo"); (1)
then(maybeFoo.get()).isEqualTo("foo");
Option<String> maybeFooBar = maybeFoo.flatMap(s -> Option.of((String)null)) (2)
                                     .map(s -> s.toUpperCase() + "bar");
then(maybeFooBar.isEmpty()).isTrue();

1	The option is `Some("foo")`
2	The resulting option is `None`

This is explored in more detail on the Vavr blog.

3.3.2. Try

Try is a monadic container type which represents a computation that may either result in an exception, or return a successfully computed value. It’s similar to, but semantically different from Either. Instances of Try, are either an instance of Success or Failure.

// no need to handle exceptions
Try.of(() -> bunchOfWork()).getOrElse(other);

import static io.vavr.API.*;        // $, Case, Match
import static io.vavr.Predicates.*; // instanceOf

A result = Try.of(this::bunchOfWork)
    .recover(x -> Match(x).of(
        Case($(instanceOf(Exception_1.class)), t -> somethingWithException(t)),
        Case($(instanceOf(Exception_2.class)), t -> somethingWithException(t)),
        Case($(instanceOf(Exception_n.class)), t -> somethingWithException(t))
    ))
    .getOrElse(other);

3.3.3. Lazy

Lazy is a monadic container type which represents a lazy evaluated value. Compared to a Supplier, Lazy is memoizing, i.e. it evaluates only once and therefore is referentially transparent.

Lazy<Double> lazy = Lazy.of(Math::random);
lazy.isEvaluated(); // = false
lazy.get();         // = 0.123 (random generated)
lazy.isEvaluated(); // = true
lazy.get();         // = 0.123 (memoized)

You may also create a real lazy value (works only with interfaces):

CharSequence chars = Lazy.val(() -> "Yay!", CharSequence.class);

3.3.4. Either

Either represents a value of two possible types. An Either is either a Left or a Right. If the given Either is a Right and projected to a Left, the Left operations have no effect on the Right value. If the given Either is a Left and projected to a Right, the Right operations have no effect on the Left value. If a Left is projected to a Left or a Right is projected to a Right, the operations have an effect.

Example: A compute() function, which results either in an Integer value (in the case of success) or in an error message of type String (in the case of failure). By convention the success case is Right and the failure is Left.

Either<String,Integer> value = compute().right().map(i -> i * 2).toEither();

If the result of compute() is Right(1), the value is Right(2).
If the result of compute() is Left("error"), the value is Left("error").

3.3.5. Future

A Future is a computation result that becomes available at some point. All operations provided are non-blocking. The underlying ExecutorService is used to execute asynchronous handlers, e.g. via onComplete(…).

A Future has two states: pending and completed.

Pending: The computation is ongoing. Only a pending future may be completed or cancelled.

Completed: The computation finished successfully with a result, failed with an exception or was cancelled.

Callbacks may be registered on a Future at each point of time. These actions are performed as soon as the Future is completed. An action which is registered on a completed Future is immediately performed. The action may run on a separate Thread, depending on the underlying ExecutorService. Actions which are registered on a cancelled Future are performed with the failed result.

// future *value*, result of an async calculation
Future<T> future = Future.of(...);

3.3.6. Validation

The Validation control is an applicative functor and facilitates accumulating errors. When trying to compose Monads, the combination process will short circuit at the first encountered error. But 'Validation' will continue processing the combining functions, accumulating all errors. This is especially useful when doing validation of multiple fields, say a web form, and you want to know all errors encountered, instead of one at a time.

Example: We get the fields 'name' and 'age' from a web form and want to create either a valid Person instance, or return the list of validation errors.

PersonValidator personValidator = new PersonValidator();

// Valid(Person(John Doe, 30))
Validation<Seq<String>, Person> valid = personValidator.validatePerson("John Doe", 30);

// Invalid(List(Name contains invalid characters: '!4?', Age must be greater than 0))
Validation<Seq<String>, Person> invalid = personValidator.validatePerson("John? Doe!4", -1);

A valid value is contained in a Validation.Valid instance, a list of validation errors is contained in a Validation.Invalid instance.

The following validator is used to combine different validation results to one Validation instance.

class PersonValidator {

    private static final String VALID_NAME_CHARS = "[a-zA-Z ]";
    private static final int MIN_AGE = 0;

    public Validation<Seq<String>, Person> validatePerson(String name, int age) {
        return Validation.combine(validateName(name), validateAge(age)).ap(Person::new);
    }

    private Validation<String, String> validateName(String name) {
        return CharSeq.of(name).replaceAll(VALID_NAME_CHARS, "").transform(seq -> seq.isEmpty()
                ? Validation.valid(name)
                : Validation.invalid("Name contains invalid characters: '"
                + seq.distinct().sorted() + "'"));
    }

    private Validation<String, Integer> validateAge(int age) {
        return age < MIN_AGE
                ? Validation.invalid("Age must be at least " + MIN_AGE)
                : Validation.valid(age);
    }

}

If the validation succeeds, i.e. the input data is valid, then an instance of Person is created of the given fields name and age.

class Person {

    public final String name;
    public final int age;

    public Person(String name, int age) {
        this.name = name;
        this.age = age;
    }

    @Override
    public String toString() {
        return "Person(" + name + ", " + age + ")";
    }

}

3.4. Collections

Much effort has been put into designing an all-new collection library for Java which meets the requirements of functional programming, namely immutability.

Java’s Stream lifts a computation to a different layer and links to a specific collection in another explicit step. With Vavr we don’t need all this additional boilerplate.

The new collections are based on java.lang.Iterable, so they leverage the sugared iteration style.

// 1000 random numbers
for (double random : Stream.continually(Math::random).take(1000)) {
    ...
}

TraversableOnce has a huge amount of useful functions to operate on the collection. Its API is similar to java.util.stream.Stream but more mature.

3.4.1. List

Vavr’s List is an immutable linked list. Mutations create new instances. Most operations are performed in linear time. Consequent operations are executed one by one.

Java 8

Arrays.asList(1, 2, 3).stream().reduce((i, j) -> i + j);

IntStream.of(1, 2, 3).sum();

Vavr

// io.vavr.collection.List
List.of(1, 2, 3).sum();

3.4.2. Stream

The io.vavr.collection.Stream implementation is a lazy linked list. Values are computed only when needed. Because of its laziness, most operations are performed in constant time. Operations are intermediate in general and executed in a single pass.

The stunning thing about streams is that we can use them to represent sequences that are (theoretically) infinitely long.

// 2, 4, 6, ...
Stream.from(1).filter(i -> i % 2 == 0);

3.4.3. Performance Characteristics

Table 1. Time Complexity of Sequential Operations
	head()	tail()	get(int)	update(int, T)	prepend(T)	append(T)
Array	const	linear	const	const	linear	linear
CharSeq	const	linear	const	linear	linear	linear
Iterator	const	const	—	—	—	—
List	const	const	linear	linear	const	linear
Queue	const	const^a	linear	linear	const	const
PriorityQueue	log	log	—	—	log	log
Stream	const	const	linear	linear	const^lazy	const^lazy
Vector	const^eff	const^eff	const ^eff	const ^eff	const ^eff	const ^eff

Table 2. Time Complexity of Map/Set Operations
	contains/Key	add/put	remove	min
HashMap	const^eff	const^eff	const^eff	linear
HashSet	const^eff	const^eff	const^eff	linear
LinkedHashMap	const^eff	linear	linear	linear
LinkedHashSet	const^eff	linear	linear	linear
Tree	log	log	log	log
TreeMap	log	log	log	log
TreeSet	log	log	log	log

Legend:

const — constant time
const^a — amortized constant time, few operations may take longer
const^eff — effectively constant time, depending on assumptions like distribution of hash keys
const^lazy — lazy constant time, the operation is deferred
log — logarithmic time
linear — linear time

3.5. Property Checking

Property checking (also known as property testing) is a truly powerful way to test properties of our code in a functional way. It is based on generated random data, which is passed to a user defined check function.

Vavr has property testing support in its io.vavr:vavr-test module, so make sure to include that in order to use it in your tests.

Arbitrary<Integer> ints = Arbitrary.integer();

// square(int) >= 0: OK, passed 1000 tests.
Property.def("square(int) >= 0")
        .forAll(ints)
        .suchThat(i -> i * i >= 0)
        .check()
        .assertIsSatisfied();

Generators of complex data structures are composed of simple generators.

3.6. Pattern Matching

Scala has native pattern matching, one of the advantages over plain Java. The basic syntax is close to Java’s switch:

val s = i match {
  case 1 => "one"
  case 2 => "two"
  case _ => "?"
}

Notably match is an expression, it yields a result. Furthermore it offers

named parameters case i: Int ⇒ "Int " + i
object deconstruction case Some(i) ⇒ i
guards case Some(i) if i > 0 ⇒ "positive " + i
multiple conditions case "-h" | "--help" ⇒ displayHelp
compile-time checks for exhaustiveness

Pattern matching is a great feature that saves us from writing stacks of if-then-else branches. It reduces the amount of code while focusing on the relevant parts.

3.6.1. The Basics of Match for Java

Vavr provides a match API that is close to Scala’s match. It is enabled by adding the following import to our application:

import static io.vavr.API.*;

Having the static methods Match, Case and the atomic patterns

$() - wildcard pattern
$(value) - equals pattern
$(predicate) - conditional pattern

in scope, the initial Scala example can be expressed like this:

String s = Match(i).of(
    Case($(1), "one"),
    Case($(2), "two"),
    Case($(), "?")
);

⚡ We use uniform upper-case method names because 'case' is a keyword in Java. This makes the API special.

Exhaustiveness

The last wildcard pattern $() saves us from a MatchError which is thrown if no case matches.

Because we can’t perform exhaustiveness checks like the Scala compiler, we provide the possibility to return an optional result:

Option<String> s = Match(i).option(
    Case($(0), "zero")
);

Syntactic Sugar

As already shown, Case allows to match conditional patterns.

Case($(predicate), ...)

Vavr offers a set of default predicates.

import static io.vavr.Predicates.*;

These can be used to express the initial Scala example as follows:

String s = Match(i).of(
    Case($(is(1)), "one"),
    Case($(is(2)), "two"),
    Case($(), "?")
);

Multiple Conditions

We use the isIn predicate to check multiple conditions:

Case($(isIn("-h", "--help")), ...)

Performing Side-Effects

Match acts like an expression, it results in a value. In order to perform side-effects we need to use the helper function run which returns Void:

Match(arg).of(
    Case($(isIn("-h", "--help")), o -> run(this::displayHelp)),
    Case($(isIn("-v", "--version")), o -> run(this::displayVersion)),
    Case($(), o -> run(() -> {
        throw new IllegalArgumentException(arg);
    }))
);

⚡ run is used to get around ambiguities and because void isn’t a valid return value in Java.

Caution: run must not be used as direct return value, i.e. outside of a lambda body:

// Wrong!
Case($(isIn("-h", "--help")), run(this::displayHelp))

Otherwise the Cases will be eagerly evaluated before the patterns are matched, which breaks the whole Match expression. Instead we use it within a lambda body:

// Ok
Case($(isIn("-h", "--help")), o -> run(this::displayHelp))

As we can see, run is error prone if not used right. Be careful. We consider deprecating it in a future release and maybe we will also provide a better API for performing side-effects.

Named Parameters

Vavr leverages lambdas to provide named parameters for matched values.

Number plusOne = Match(obj).of(
    Case($(instanceOf(Integer.class)), i -> i + 1),
    Case($(instanceOf(Double.class)), d -> d + 1),
    Case($(), o -> { throw new NumberFormatException(); })
);

So far we directly matched values using atomic patterns. If an atomic pattern matches, the right type of the matched object is inferred from the context of the pattern.

Next, we will take a look at recursive patterns that are able to match object graphs of (theoretically) arbitrary depth.

Object Decomposition

In Java we use constructors to instantiate classes. We understand object decomposition as destruction of objects into their parts.

While a constructor is a function which is applied to arguments and returns a new instance, a deconstructor is a function which takes an instance and returns the parts. We say an object is unapplied.

Object destruction is not necessarily a unique operation. For example, a LocalDate can be decomposed to

the year, month and day components
the long value representing the epoch milliseconds of the corresponding Instant
etc.

3.6.2. Patterns

In Vavr we use patterns to define how an instance of a specific type is deconstructed. These patterns can be used in conjunction with the Match API.

Predefined Patterns

For many Vavr types there already exist match patterns. They are imported via

import static io.vavr.Patterns.*;

For example we are now able to match the result of a Try:

Match(_try).of(
    Case($Success($()), value -> ...),
    Case($Failure($()), x -> ...)
);

⚡ A first prototype of Vavr’s Match API allowed to extract a user-defined selection of objects from a match pattern. Without proper compiler support this isn’t practicable because the number of generated methods exploded exponentially. The current API makes the compromise that all patterns are matched but only the root patterns are decomposed.

Match(_try).of(
    Case($Success($Tuple2($("a"), $())), tuple2 -> ...),
    Case($Failure($(instanceOf(Error.class))), error -> ...)
);

Here the root patterns are Success and Failure. They are decomposed to Tuple2 and Error, having the correct generic types.

⚡ Deeply nested types are inferred according to the Match argument and not according to the matched patterns.

User-Defined Patterns

It is essential to be able to unapply arbitrary objects, including instances of final classes. Vavr does this in a declarative style by providing the compile time annotations @Patterns and @Unapply.

To enable the annotation processor the artifact vavr-match needs to be added as project dependency.

⚡ Note: Of course the patterns can be implemented directly without using the code generator. For more information take a look at the generated source.

import io.vavr.match.annotation.*;

@Patterns
class My {

    @Unapply
    static <T> Tuple1<T> Optional(java.util.Optional<T> optional) {
        return Tuple.of(optional.orElse(null));
    }
}

The annotation processor places a file MyPatterns in the same package (by default in target/generated-sources). Inner classes are also supported. Special case: if the class name is $, the generated class name is just Patterns, without prefix.

Guards

Now we are able to match Optionals using guards.

Match(optional).of(
    Case($Optional($(v -> v != null)), "defined"),
    Case($Optional($(v -> v == null)), "empty")
);

The predicates could be simplified by implementing isNull and isNotNull.

⚡ And yes, extracting null is weird. Instead of using Java’s Optional give Vavr’s Option a try!

Match(option).of(
    Case($Some($()), "defined"),
    Case($None(), "empty")
);

4. License

Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at

http://www.apache.org/licenses/LICENSE-2.0

Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.